[CS] 비트와 이진법
CS 정리 2P
bit (비트)
binary digit의 약자로, 컴퓨터에서 정보를 표현하는 가장 작은 단위이다.
비트는 0(고)과 1(저)의 두 가지 값만 가질 수 있으며, 모든 디지털 데이터는 이러한 비트의 조합으로 이루어진다.
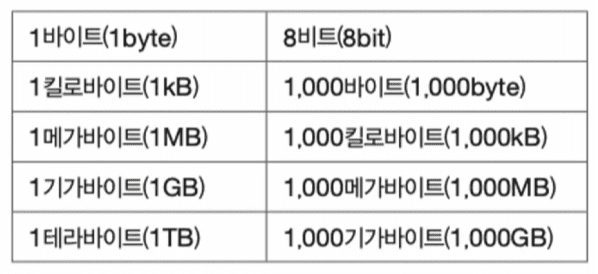
여러 비트가 모여 byte(바이트)를 형성하며, 1바이트는 8비트로 구성된다.
비트의 역할
정보 표현
- 텍스트, 이미지, 오디오, 비디오 등 모든 형태의 데이터는 비트의 조합으로 표현된다.
- 문자 ‘A’는 01000001 (8비트)로 표현된다.
연산 수행
- 컴퓨터의 중앙 처리 장치(CPU)는 비트 단위로 데이터를 처리한다.
- 기본적인 논리 연산(AND, OR, NOT)과 산술 연산(덧셈, 뺄셈 등)을 비트를 이용해 수행한다.
Binary (이진법)
숫자를 0과 1의 두 가지 숫자로만 표현하는 수 체계이다.
이진법은 컴퓨터와 디지털 시스템의 기본적인 수 체계로, 모든 데이터와 명령어가 이진법을 통해 표현되어 처리된다.
이진법의 개념

- 이진법은 숫자를 0과 1의 두 가지 상태로 표현한다.
- 각 자릿수는 2의 거듭제곱을 기반으로 한다.
- 이진수의 각 자리 값은 오른쪽에서 왼쪽으로 2^0, 2^1, 2^2, 2^3, … 순으로 증가한다.
- 이진수 1101의 각 자리 값은 2^3, 2^2, 2^1, 2^0로 각각 8, 4, 2, 1을 나타낸다.
이진수 표현 방법
숫자 변환
십진수(10진법) 13을 이진수로 변환하는 방법:
- 13을 2로 나누면 몫이 6, 나머지가 1
- 6을 2로 나누면 몫이 3, 나머지가 0
- 3을 2로 나누면 몫이 1, 나머지가 1
- 1을 2로 나누면 몫이 0, 나머지가 1
- 나머지를 역순으로 배열하면 1101이 된다.
이진수 덧셈
이진수의 덧셈은 십진수의 덧셈과 유사하지만, 2를 넘으면 자리 올림이 발생한다.
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
- 1 + 1 + 1 = 11
1010
+ 1101
------
10111 (23)
- 첫 번째 자리 (오른쪽에서 첫 번째 비트): 0 + 1 = 1
- 두 번째 자리: 1 + 0 = 1
- 세 번째 자리: 0 + 1 = 1
- 네 번째 자리: 1 + 1 = 10
이진수 뺄셈
이진수의 뺄셈도 자리 발림을 사용하여 수행된다.
- 0 - 0 = 0
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 = 1
1101 (13)
- 1010 (10)
---------
0011 (3)
- 첫 번째 자리: 1 - 0 = 1
- 두 번째 자리: 0 - 1 = 1 (빌림이 필요, 왼쪽 자리에서 1 빌림)
- 세 번째 자리: 1 - 0 = 1 (빌려주기 전에 1 - 1 + 1(빌림) = 1)
- 네 번째 자리: 1 - 1 = 0
이진법으로 음수를 표현하는 방법
가장 일반적인 방법은 Two’s Complement(2의 보수) 표현을 사용하는 것이다.
- 양의 이진수를 1의 보수로 변환: 모든 비트를 반전시킨다. (0을 1로, 1을 0으로)
- 1의 보수에 1을 더하여 2의 보수를 구함: 1의 보수에 1을 더한다.
- 예: -3을 2의 보수로 표현
- 십진수 3을 이진수로 변환: 3 → 0011
- 1의 보수로 변환: 0011 → 1100
- 1의 보수에 1을 더함: 1100 + 1 → 1101 따라서, 4비트 시스템에서 -3은 1101로 표현된다.
2의 보수를 이용한 덧셈과 뺄셈
2의 보수를 사용하면 음수와 양수의 덧셈 및 뺄셈을 동일한 방식으로 수행할 수 있다.
0101 (5)
+ 1101 (-3)
--------
10010
5비트 결과에서 4비트만 취함: 0010 (2)
따라서, 5 + (-3) = 2이다.
MSB (Most Significant Bit)
이진수에서 가장 중요한 자리의 비트를 의미한다.
가장 왼쪽에 위치한 비트로, 숫자의 부호(양수 또는 음수)나 크기에 큰 영향을 미친다.
- Sign Bit(부호 비트)
- 특히 2의 보수 표현에서 MSB는 숫자의 부호를 나타낸다.
- MSB가 0이면 양수, 1이면 음수이다.
- 0101 (5)에서 MSB는 0, 따라서 양수이다.
- 1101 (-3)에서 MSB는 1, 따라서 음수이다.
- 숫자의 크기 결정
- MSB는 가장 높은 값을 가지는 자리이므로 숫자의 크기를 결정하는 데 큰 영향을 미친다.
- 예를 들어, 8비트 숫자에서 MSB는 2^7(128)의 값을 가진다.
이진법의 활용
컴퓨터 내부 처리
- 컴퓨터는 전기적 신호의 두 가지 상태(ON/OFF, 1/0)를 사용하여 데이터를 처리하므로 이진법이 적합하다.
- 모든 데이터(문자, 이미지, 소리 등)는 이진수로 변환되어 처리된다.
메모리 주소 지정
- 메모리의 각 주소는 이진수로 표현된다.
- CPU가 메모리의 특정 위치에 접근할 때 이진 주소를 사용한다.
디지털 통신
- 네트워크와 통신 시스템에서는 이진수로 데이터를 전송한다.
- 신호를 0과 1로 변환하여 전송하고, 수신 측에서 이를 다시 해석한다.
이진법과 다른 수 체계의 변환
십진수에서 이진수로 변환
앞서 설명한 대로, 십진수를 2로 나누어 나머지를 구하고 이를 역순으로 배열한다.
이진수에서 십진수로 변환
이진수의 각 자리 값을 2의 거듭제곱으로 변환한 후 합산한다.
이진수 1101은 (1 x 2^3) + (1x2^2) + (0x2^1) + (1 x 2^0)
즉 8 + 4 + 0 + 1 = 13이다.
이진수에서 십육진수로 변환
이진수를 4자리씩 묶어 각 묶음을 십육진수로 변환한다.
이진수 10101100은 1010(A)와 1100(C)으로 나뉘어 AC(십육진수)가 된다.
십육진수에서 이진수로 변환
각 십육진수 자리를 4비트의 이진수로 변환한다.
십육진수 1F는 1(0001)과 F(1111)로 변환되어 00011111이 된다.

댓글남기기